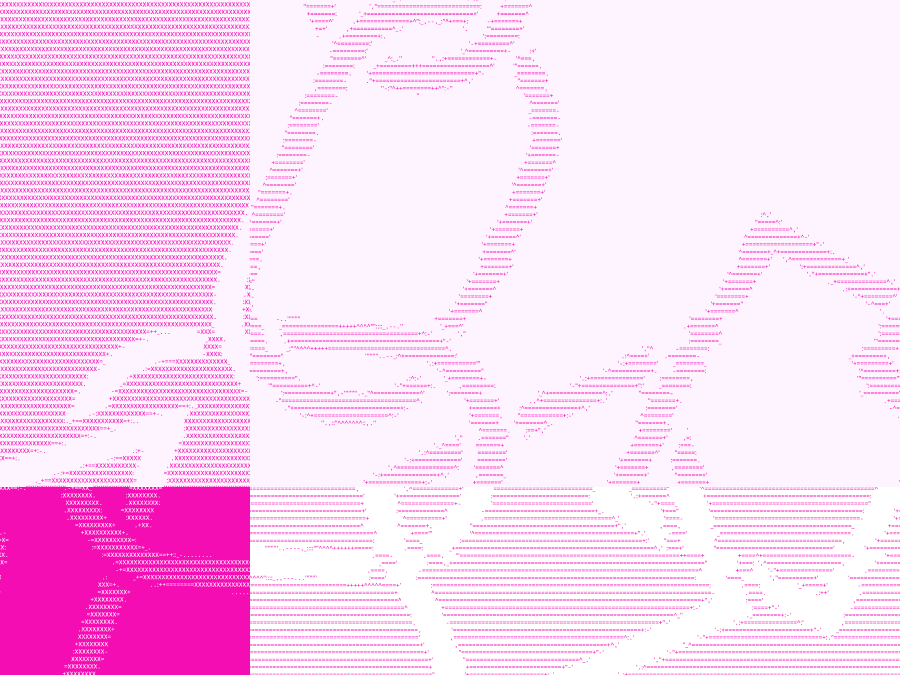By: Austin Adams, Sara Reynolds, and Rachel Eichenberger 1
Uniswap Protocol makes swapping simple and accessible, but its math may not be. To help developers building on the Protocol, analysts drawing insights, and researchers studying market activity, let’s dig into a few of the most common technical questions we see.
- What is Q Notation?
- How do I calculate the current exchange rate?
- How do tick and tick spacing relate to sqrtPrice?
Part 2 focuses on:
- Working with virtual liquidity
- Calculating LP holdings
- Calculating uncollected fees in a position

What is a Q notation?
If you've ever read the Uniswap v3 code and seen variables that end with X96 or X128, you have come across what we call Q notation. With Uniswap v3 came the heavy usage of the Q notation to represent fractional numbers in fixed point arithmetic. If that seems like word salad to you, then don't worry!
Long story short, you can convert from Q notation to the “actual value” by dividing by where is the value after the X. For example, you can convert sqrtPriceX96 to sqrtPrice by dividing by
Q notation specifies the parameters of the binary fixed point number format, which allows variables to remain integers, but function similarly to floating point numbers. Variables that must be as precise as possible in Uniswap v3 are represented with a maximum of 256 bits and account both for overflow and potential rounding issues. By using Q notation, the protocol can ensure that granular decimal precision is not lost.
Code example
// Get sqrtPriceX96 from token reserves
// In scripts that use Javascript, we are limited by the size of numbers with a max of 9007199254740991. Since crypto
// handles everything in lowest decimal format, We have to use a version of BigNumber, allowing Javascript to handle
// numbers that are larger than the max.
// Here we use a Pure BigNumber script from EthersJS along with BigNumber itself
// you will also see us use JSBI is a pure-JavaScript implementation of the official ECMAScript BigInt proposal
import { BigNumber } from 'ethers'; // ← used to convert bn object to Ethers BigNumber standard
import bn from 'bignumber.js' // ← here we use BigNumber pure to give us more control of precision
// and give access to sqrt function
//bn.config allows us to extend precision of the math in the BigNumber script
bn.config({ EXPONENTIAL_AT: 999999, DECIMAL_PLACES: 40 })
function encodePriceSqrt(reserve1, reserve0){
return BigNumber.from(
new bn(reserve1.toString()).div(reserve0.toString()).sqrt()
.multipliedBy(new bn(2).pow(96))
.integerValue(3)
.toString()
)
}
// reserve1 , reserve0
encodePriceSqrt(1000000000000000000, 1539296453)
How do I calculate the current exchange rate?
One of the first questions people naturally ask in a market is “what is the current price”? For Uniswap v3, the price is quoted as the current exchange from token 0 to token 1 and is found in sqrtPriceX96.
Uniswap v3 shows the current price of the pool in slot0. slot0 is where most of the commonly accessed values are stored, making it a good starting point for data collection. You can get the price from two places; either from the sqrtPriceX96 or calculating the price from the pool tick value2. Using sqrtPriceX96 should be preferred over calculating the price from the current tick, because the current tick may lose precision due to the integer constraints (which will be discussed more in depth in a later section).
sqrtPriceX96 represents the sqrtPrice times as described in the Q notation section. was specifically was chosen because it was the largest value for precision that allowed the protocol team to squeeze the most variables into the contract storage slot for gas efficiency.
Math
First, as previously discussed, sqrtPrice is the sqrtPriceX96 of the pool divided by .
You can convert the sqrtPrice of the pool into the price of the pool by squaring the sqrtPrice.
Putting those equations together
Math Example
In the USDC-WETH 5-bps pool (also the .05% fee tier), token0 for this pool is USDC and token 1 is WETH. For this pool, . This also represents the exchange rate from to . For this specific pool, this exchange rate is the amount of WETH that could be traded for 1 USDC3.
From slot0 in the pool contract at address 0x88e6a0c2ddd26feeb64f039a2c41296fcb3f5640 at block number 15436494.
Plugging this value into the equation above, we have
erc20 tokens have built in decimal values. For example, 1 WETH actually represents WETH in the contract whereas USDC is . Therefore, USDC has 6 decimals and WETH has 18.
Most exchanges quote the multiplicative inverse, which is the amount of USDC that represents 1 WETH. To adjust for this, we also need to divide as
This is the number generally seen quoted on exchanges and data sources. See the formula and math here: Symbolab Big Math
Code Example
This will give the price of both tokens in relation to the other, as all pools will have two prices.
// Get the two token prices of the pool
// PoolInfo is a dictionary object containing the 4 variables needed
// {"SqrtX96" : slot0.sqrtPriceX96.toString(), "Pair": pairName, "Decimal0": Decimal0, "Decimal1": Decimal1}
// to get slot0 call factory contract with tokens and fee,
// then call the pool slot0, sqrtPriceX96 is returned as first dictionary variable
// var FactoryContract = new ethers.Contract(factory, IUniswapV3FactoryABI, provider);
// var V3pool = await FactoryContract.getPool(token0, token1, fee);
// var poolContract = new ethers.Contract(V3pool, IUniswapV3PoolABI, provider);
// var slot0 = await poolContract.slot0();
function GetPrice(PoolInfo){
let sqrtPriceX96 = PoolInfo.SqrtX96;
let Decimal0 = PoolInfo.Decimal0;
let Decimal1 = PoolInfo.Decimal1;
const buyOneOfToken0 = ((sqrtPriceX96 / 2**96)**2) / (10**Decimal1 / 10**Decimal0).toFixed(Decimal1);
const buyOneOfToken1 = (1 / buyOneOfToken0).toFixed(Decimal0);
console.log("price of token0 in value of token1 : " + buyOneOfToken0.toString());
console.log("price of token1 in value of token0 : " + buyOneOfToken1.toString());
console.log("");
// Convert to wei
const buyOneOfToken0Wei =(Math.floor(buyOneOfToken0 * (10**Decimal1))).toLocaleString('fullwide', {useGrouping:false});
const buyOneOfToken1Wei =(Math.floor(buyOneOfToken1 * (10**Decimal0))).toLocaleString('fullwide', {useGrouping:false});
console.log("price of token0 in value of token1 in lowest decimal : " + buyOneOfToken0Wei);
console.log("price of token1 in value of token1 in lowest decimal : " + buyOneOfToken1Wei);
console.log("");
}
// WETH / USDC pool 0.05% →(1% == 10000, 0.3% == 3000, 0.05% == 500, 0.01 == 100)
("0xC02aaA39b223FE8D0A0e5C4F27eAD9083C756Cc2", "0xA0b86991c6218b36c1d19D4a2e9Eb0cE3606eB48", 500)
// Output
price of token0 in value of token1 : 1539.296453
price of token1 in value of token0 : 0.000649647439939888
price of token0 in value of token1 in lowest decimal : 1539296453
price of token1 in value of token1 in lowest decimal : 649647439939888
Relationship between tick and sqrtPrice
Ticks are used in Uniswap v3 to determine the liquidity that is in-range. Uniswap v3 pools are made up of ticks ranging from -887272 to 887272, which functionally equate to a token price between 0 and infinity4, respectively. More on this below.
Ticks vs Tick-Spacing
We find that end users are constantly confused by ticks vs tick-spacing.
- Ticks: Units of measurement that are used to define specific price ranges
- Tick-spacing: The distance between two ticks, as defined by the fee tier
Not every tick can be initialized. Instead, each pool is initialized with a tick-spacing that determines the space between each tick. Tick-spacings are also important to determine where liquidity can be placed or removed. If there is an initialized tick at tick 202910, then liquidity at most can change as early as the first value given by the tick-spacing, which is 202910 + 10 for the 5 bps pool5.
Table 1. Relationship between fees and tick-spacing

Using the table above, we can determine the tick-spacing of the pool directly from the fee-tier. We show both the percentage and the bps format for these values, as used interchangeably by practitioners, but may be confusing for new users.
Figure 1. Example of tick-spacing vs ticks for WETH-USDC 5 bps pool

In Figure 1, we show a small portion of the liquidity distribution for the WETH-USDC 5 bps pool at the block previously discussed. The dashed black lines indicate possible initialized ticks (which occur every at minimum tick-spacing of 10 for 5 bps pools). The solid black line indicates the current tick of the pool.
Also notice that liquidity is constant between two dashed lines. This is because liquidity can only change when a tick-spacing is crossed. Between those ticks, the liquidity in-range is treated like an xy=k curve like Uniswap v2 for trading. If that confuses you, don't worry, it's not important. If you want to learn more about liquidity, we will talk more about liquidity in a later post.
What does a tick represent?
Ticks are related directly to price. To convert from tick , to price, take 1.0001 to get the corresponding price. Let the tick-spacing be and be the lower bound of the active tick-range, then the current tick-range is We can then map the current tick-range to the current price-range with
Note: Everything up-to, but not including the upper tick is part of the current range
While liquidity can only be added at initialized ticks, the current market-price can be between initialized ticks. In the example above, the USDC-WETH 5-bps pool is at tick 202919. This number is not evenly divisible by the tick-spacing of 10, we need to find the nearest numbers above and below that are. This corresponds to tick 202910 and tick 202920, which we showed in Figure 1.
The current tick-range can also be calculated by 6
In the USDC-WETH example we get:
Thus, the current tick-range of in-range liquidity for the USDC-WETH pool is currently , but what prices does this tick-range map to? Its maps to
Let's convert to tick-range in terms of adjusted as done previously. Remember that we need to adjust for the decimal differences between USDC and WETH, and invert the price since we want (the amount of USDC given by 1 WETH) not (the amount of WETH given by 1 USDC).
The price we calculated from sqrtPriceX96 in the previous example falls between this range - a good sanity check that we've calculated the price ranges properly!7
How does tick and tick spacing relate to sqrtPriceX96?
You may be asking, if (the current tick of the pool) and (derived from the sqrtPriceX96 of the pool) then why does
Instead of calculating the price using the tick value from the slot0 call, let's derive it from the sqrtPriceX96 value and see where the discrepancy between the current tick and sqrtPriceX96 lies.
We know that , then
This explains why using ticks can be less precise than sqrtPriceX96 in Uniswap v3.
Just like ticks can be in between initialized ticks, ticks can also be in-between integers as well! The protocol itself reports the floor of the current tick, which the sqrtPriceX96 retains.
Example Tick to Price
let price0 = (1.0001**tick)/(10**(Decimal1-Decimal0))
let price1 = 1 / price0
Example sqrtPriceX96 to Tick
Note: the Math.floor as stated above, the calculation will have decimals, not needed for tick
const Q96 = JSBI.exponentiate(JSBI.BigInt(2), JSBI.BigInt(96));
let tick = Math.floor(Math.log((sqrtPriceX96/Q96)**2)/Math.log(1.0001));
Conclusion
Overall, we hope that this long primer on Uniswap v3 is helpful. Helping our community gracefully and efficiently understand Uniswap v3 will help push along the ecosystem to be the best that it can be. For anything else, feel free to join the dev-chat in our discord and ask.
Read part 2 here.
Related References
- Liquidity Math in Uniswap v3 by Atis Elsts
- Uniswap v3 Development Book by Ivan Kuznetsov
- Uniswap v3 Core by the Uniswap Labs' team
- Uniswap v3 - New Era of AMMs? By Finematics
Footnotes
-
We thank Atis Elsts for their comments. ↩
-
price = , and this equation will be explained more later in the blog post. ↩
-
It is important to note that this is backwards to what people expect, which is a problem that many developers run into. Uniswap v3 chooses token ordering by their contract address, and the USDC contract address comes first. ↩
-
This conversion from tick to price directly equates to to , which are functionally 0 to infinity. ↩
-
Ticks are only initialized if someone has placed liquidity that either starts or ends at that tick. It is possible that no one placed liquidity ending at the next tick, so it may not be initialized. However, positions can only be placed at ticks that are determined by the tick-spacing. ↩
-
represents the floor of the value , or the greatest integer value that is less than or equal to ↩
-
Notice that the larger price is now first. That is because of the inverting of the exchange rate. This can cause a lot of confusion and problems with code! ↩